横浜国立大学　電磁気　H20~29

H25年度　H26年度　H27年度　H28年度　H29年度

---

平成25年度

(1) \begin{align} a \leqq r \leqq bで\\ E=\frac{Q}{4πε_0r^2}[V/m]\\ 電位差V_{12}=-\int _a^b \frac{Q}{4πε_0r^2}dr\\ =\frac{Q}{4πε_0} \left( \frac{1}{a}-\frac{1}{b} \right) \underline{= \frac{Q(b-a)}{4πε_0ab}[V]}\\ \end{align} (2) \begin{align} 磁束密度B = \frac{μNI}{2πr}\\ 磁束\phi = c\int _a^b \frac{μNI}{2πr}dr =\underline{ \frac{μcNI}{2π}ln\frac{b}{a}[Wb]}\\ \end{align}

---

平成26年度

(1) \begin{align} 電荷密度\sigma _v=\frac{3Q}{4πa^3}[C/m^3]\\ i)0 \leqq r \lt a \\ E = \frac{\sigma_v}{4πε_0r^2}・\frac{4}{3}πr^3=\underline{\frac{rQ}{4πε_0a^3}[V/m]}\\ ii)a \lt r\\ E =\underline{ \frac{Q}{4πε_0r^2}[V/m]}\\ \end{align}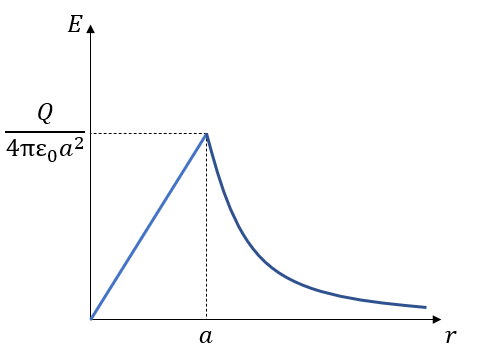

(2) \begin{align} 内導体に電流Iを流し、外導体に電流-Iの電流を流した時、\\ a \leqq r \leqq bで\\ B=\frac{μ_0I}{2πr}\\ \phi =\int _a^b Bdr=\frac{μ_0I}{2π}ln\frac{b}{a}\\ \therefore 自己インダクタンスL=\frac{\phi}{I}=\underline{\frac{μ_0}{2π}ln\frac{b}{a}[H/m]}\\ \end{align} (3) \begin{align} e = \frac{d\varphi}{dt}=\phi_0\\ I=\frac{e}{R}=\frac{\phi_0}{R}\\ 電荷が通過した量なのでq=\underline{\frac{\phi_0}{R}[C]}\\ \end{align}

---

平成27年度

(1) \begin{align} 内導体に+Q,外導体に-Q[C]の電荷を印加したとすると、\\ a \leqq r \leqq bで\\ E=\frac{Q}{2πε_0rL}\\ V=\frac{Q}{2πε_0L}・-\int_b^a\frac{1}{r}dr=\frac{Q}{2πε_0L}ln\frac{b}{a}\\ C=\frac{Q}{V}=\underline{\frac{2πε_0L}{ln\frac{b}{a}}[F]}\\ \end{align} (2) \begin{align} 0\leqq r \lt b:H=0\\ b \leqq r \lt c:H=\frac{J}{2πr}\pi (r^2-b^2)=\frac{J}{2}\left( r-\frac{b^2}{r} \right)[A/m]\\ c \leqq r :H=\frac{J}{2r}(c^2-b^2)[A/m]\\ \end{align}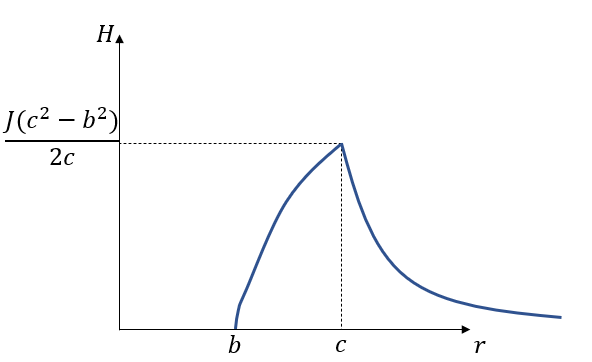

---

---

平成28年度

(1) \begin{align} a \leqq r \leqq b\\ E=\frac{Q}{2\pi ε_0r}[V/m]\\ V_{ab}=-\int _b^a Edr=\frac{Q}{2\pi ε_0}ln\frac{b}{a}[V]\\ C=\frac{Q}{V}=\underline{\frac{2\pi ε_0}{ln\frac{b}{a}}[F]}\\ \end{align} (2) \begin{align} y方向成分は打ち消されるので\\ dH_x=\frac{Idl}{4\pi(r^2+x^2)}・\frac{r}{\sqrt{r^2+x^2}}\\ \therefore H=\int _0^{2\pi r}dH_x =\underline{\frac{Ir^2}{2(r^2+x^2)^{2/3}}[A/m]}\\ \end{align}

---

平成29年度

(1) \begin{align} a \leqq r \leqq b で\\ E=\frac{Q}{2\pi ε_0 r}\\ 電位差V=-\int _b^a \frac{Q}{2\pi ε_0r}dr=\frac{Q}{2\pi ε_0}ln\frac{b}{a}\\ \therefore C=\frac{Q}{V}=\underline{\frac{2\pi ε_0}{ln\frac{b}{a}}[F]}\\ \end{align} (2) \begin{align} a \leqq r \leqq b で\\ B=\frac{μ_0I}{2\pi r}\\ \phi =\int_a^b\frac{μ_0I}{2\pi r}dr=\frac{μ_0I}{2\pi}ln\frac{b}{a}\\ \therefore L=\frac{\phi}{I}=\underline{\frac{μ_0}{2\pi}ln\frac{b}{a}[H/m]}\\ \end{align} (3) \begin{align} (1)(2)より\\ \frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{\frac{2\pi ε_0}{ln(b/a)}・\frac{μ_0}{2\pi}ln\frac{b}{a}}}=\frac{1}{\sqrt{ε_0μ_0}}=\frac{1}{\sqrt{\frac{10^{-16}}{9}}}=\underline{3×10^8}\\ \frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{\frac{V}{dI/dt}・\frac{Q}{V}}}=\frac{1}{\sqrt{\frac{Q}{d^2Q/dt^2}}}\left[ \frac{1}{\sqrt{\frac{C}{C/s^2}・\frac{1}{m^2}}}\right] =\underline{[m/s]}\\ \end{align}