目次
平成20年度(応用物理Ⅰ)
反時計回りを正とする。 (1) \begin{align} i)0 \leqq r \leqq a \\ \underline{B=0}\\ ii)a \lt r \leqq 2a \\ \underline{B=\frac{μ_0I}{2πr}[T]}\\ iii)2a\lt r\\ \underline{B=\frac{μ_0・2I}{2πr}=\frac{μ_0I}{πr}[T]}\\ \end{align} (2) \begin{align} i)0 \leqq r \leqq a\\ \underline{B=\frac{0}{2πr}=0}\\ ii)a \lt r \leqq 2a \\ \underline{B=\frac{μ_0I}{2πr}[T]}\\ iii)2a\lt r\\ \underline{B=0}\\ \end{align} (3) \begin{align} i)0 \leqq r \leqq a\\ \underline{B=0}\\ ii)a \lt r \leqq 2a \\ \underline{B=\frac{μ_0I}{2πr}[T]}\\ iii)2a\lt r\\ \underline{B=-\frac{μ_0I}{2πr}[T]}\\ \end{align}平成21年度
(1) \begin{align} クーロン力が各電荷にかかる。\\ 各電荷に働く力の大きさFは\\ F=\frac{Q^2}{8πε_0a^2}+\sqrt{\frac{2Q^4}{16(πε_0a^2)^2}}=\underline{\frac{Q^2(1+2\sqrt{2})}{8πε_0a^2}[N]}\\ \end{align} (2) \begin{align} 誘電体挿入前の容量C_0は\\ C_0=\frac{Q}{V},V=Ed=\frac{Q}{ε_0S}d\\ \therefore \underline{C_0=\frac{S}{d}ε_0}\\ 誘電体挿入後の容量Cは、誘電体挿入部の\\ 容量C_1と誘電体非挿入部の容量C_2の和で表されるので\\ C_1=\frac{3ε_0S}{4d},C_2=\frac{ε_0ε_rS}{4d}\\ \therefore C=C_1+C_2=\frac{ε_0S}{4d}(3+ε_r)[F]\\ 変化量 \Delta C=C-C_0=\underline{\frac{ε_0S}{4d}(ε_r-1)[F]}\\ \end{align} (3) \begin{align} 導線3,4により導線1,2間に発生する磁束B_3,B_4の大きさは、\\ B_3=\frac{μ_0I}{2πr}[Wb],B_4=\frac{μ_0I}{2π(r+d)}[T]\\ よって、距離rに発生する磁束Bは、\\ B=B_3-B_4=\frac{μ_0I}{2π}\left(\frac{1}{r}-\frac{1}{r+d}\right)\\ 磁束鎖交数\phi =\int _{D-d}^{D} B dr=\frac{μ_0I}{2π}\left[ ln\frac{r}{r+d}\right] _{D-d}^{D}\\ =\frac{μ_0I}{2π}ln\frac{D^2}{D^2-d^2}[Wb]\\ \therefore 相互インダクタンスM=\frac{\phi}{I}=\underline{\frac{μ_0}{2π}ln\frac{D^2}{D^2-d^2}[H/m]}\\ \end{align}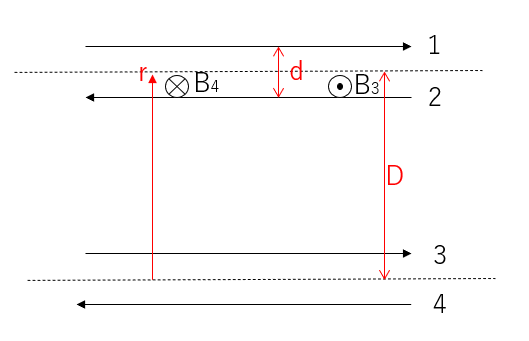
平成22年度(電磁気学)
(1) \begin{align}クーロン則より、\\ Q_1に働く力F_1=\frac{Q_1Q_2}{4πε_0a^2}+\frac{Q_1Q_3}{4πε_04a^2}=\underline{\frac{Q_1}{4πε_0a^2}\left(Q_2+\frac{Q_3}{4}\right)[N]}\\ Q_2に働く力F_2=\frac{Q_2Q_3}{4πε_0a^2}-\frac{Q_1Q_2}{4πε_0a^2}=\underline{\frac{Q_2(Q_3-Q_1)}{4πε_0a^2}[N]}\\ Q_3に働く力F_3=-\frac{Q_2Q_3}{4πε_0a^2}-\frac{Q_1Q_2}{4πε_0・4a^2}=\underline{-\frac{Q_3}{4πε_0a^2}\left(Q_2+\frac{Q_1}{4}\right)[N]}\\ \end{align} (2) \begin{align} 中心軸上における磁束密度をx成分とy成分に分けるとy成分は打ち消され、x成分だけが残る\\ 距離b[m]だけ離れた地点の磁束密度B_bは、ビオサバール則より\\ dB_b=dB_{bx}=\frac{μ_0INdl}{4π(b^2+a^2)}・\frac{a}{\sqrt{b^2+a^2}}=\frac{μ_0aIN}{4π(b^2+a^2)^{3/2}}dl\\ \therefore B_b=\int_0^{2πa}\frac{μ_0aIN}{4π(b^2+a^2)^{3/2}}dl=\underline{\frac{μ_0a^2IN}{2(a^2+b^2)^{3/2}}[T]}\\ 点Oでは、b=0より、\\ B_O=\frac{μ_0a^2I}{2a^3}=\underline{\frac{μ_0IN}{2a}[T]}\\ \end{align}平成23年度(電磁気学)
(1) \begin{align} V_p=\frac{Q}{4πε_0・2}+\frac{3Q}{4πε_0・2}=\underline{\frac{Q}{2πε_0}[V]}\\ \end{align} (2) \begin{align} 円環鉄心内に発生する磁束密度Bは、\\ B=\frac{μnI}{2πr_0}[T]\\ 磁束鎖交数\phi=BAn=\frac{μn^2AI}{2πr_0}[Wb]=LI[Wb]\\ \therefore L=\frac{μn^2A}{2πr_0}\\ e=L\frac{dI}{dt}より、V_0cosωt=L\frac{dI}{dt}\\ \therefore \frac{dI}{dt}=\frac{2πr_0V_0}{μn^2A}cosωt\\ \therefore \underline{I=\frac{2πr_0V_0}{μn^2ωA}sinωt[A]}\\ \underline{B=\frac{V_0}{Aω}sinωt[T]}\\ \end{align}平成24年度
(1) \begin{align} a\leqq r\leqq bで導体に+Q[C]の電荷を帯電させたとき、\\ E=\frac{Q}{4πεr^2}\\ V=\frac{Q}{4πε_0b}+\frac{Q}{4πε}\left(\frac{1}{r}-\frac{1}{b}\right)\\ r=aでは、V=\frac{Q}{4πε_0b}+\frac{Q(b-a)}{4πεab}\\ C=\frac{Q}{V}より、\\ C=4πb\frac{1}{\frac{1}{ε_0}+\frac{b-a}{εa}}=\underline{\frac{4πε_0εab}{εa+ε_0(b-a)}[F]}\\ \end{align} (2) \begin{align} (a)\\ l \gg aより、無限長なソレノイドであると考えると、\\ 単位長さ当たりの巻き数n=\frac{N}{l}\\ \therefore 磁束密度B=μnI=μ_0\frac{N}{l}I[T] 磁束鎖交数Φ=BSN=\frac{μ_0N^2πa^2I}{l}\\ 自己インダクタンス\underline{L=\frac{\phi}{I}=\frac{πμ_0N^2a^2}{l}[H]}\\ (b)\\ 磁気エネルギーW_m=\frac{1}{2}LI^2より、\\ W_m=\frac{μ_0N^2πa^2I^2}{2l}[J]\\ 仮想変位の力の式を用いて\\ 軸方向への力\underline{F_1=+\frac{ \partial W_m }{ \partial a }=\frac{πμ_0N^2aI^2}{l}[N]}\\ 径方向への力\underline{F_2=-\frac{ \partial W_m }{ \partial l }=\frac{πμ_0N^2a^2I^2}{2l^2}[N]}\\ \end{align}ページ: 1 2